Les coûts élevés du prolongement de la ligne bleue vers Anjou s’expliquent par de nouvelles règles comptables et par la complexité du projet, avance la Société de transport de Montréal (STM) qui tenait un breffage technique sur le sujet, lundi.
Depuis que les estimations du coût des travaux – 3,9G$ pour cinq stations – ont été dévoilées le mois dernier, plusieurs ont souligné qu’elles étaient bien plus élevées que la facture du prolongement de la ligne orange réalisé il y a dix ans. L’ancien élu Richard Bergeron a notamment souligné que le coût au kilomètre est quatre fois plus élevé pour le prolongement de la ligne bleue (672M$ par kilomètre) que pour celui pour la ligne orange vers Laval (environ 170M$ par kilomètre, inflation incluse).
«Je soupçonne qu’avec le prolongement de la ligne bleue du métro, nous sommes en présence d’un délire d’ingénieurs trop heureux d’avoir fait sauter la banque. Comme cela fait plus de 30 ans que les Montréalais attendent ce prolongement, personne n’ose discuter les chiffres avancés», a-t-il écrit dans une lettre ouverte publiée en mars sur LaPresse+, en demandant une comptabilité détaillée permettant d’y voir plus clair.
C’est ce que s’est proposé de faire lundi François Chamberland, directeur exécutif de l’ingénierie, des infrastructures et des projets majeurs à la STM. S’il convient que le prolongement vers Laval a coûté moins cher (751M$), il précise que réaliser le même projet autour de 2024 coûterait 293M$ de plus à cause de l’inflation.
Ce n’est pas tout. «À Laval, on a surtout construit sur des terrains vacants alors que pour Anjou, on travaille dans un secteur à haute densité commerciale. Alors, on a prévu 361M$ de plus pour les expropriations», a-t-il ajouté. Sur les 45 terrains ou immeubles à exproprier, 24 appartiennent à des propriétaires privés.
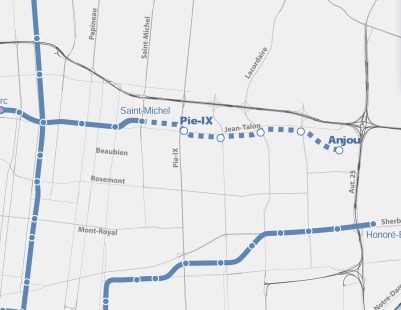
Il y a en outre un tunnel piétonnier de 69M$ à construire sous le boulevard Pie-IX pour rejoindre l’un des arrêts du futur système rapide par bus, qui doit être mis en service en 2022, si le conseil des ministres autorise le plan d’affaires.
Sans compter que depuis le prolongement de la ligne orange sur l’île Jésus, les règles comptables entourant les grands projets doivent désormais englober les coûts complets et pas uniquement les coûts directs. «Rien que pour les frais financiers sur les emprunts, ce sont 617M$ qui sont comptabilisés pour la ligne bleue, alors que pour le prolongement de la ligne orange, ils ont été comptabilisés à part par le gouvernement», a mentionné M. Chamberland.
Parmi les aspects techniques, le prolongement vers Anjou compte deux stations intermodales (contre une seule à Laval), plus d’édicules secondaires (+93M$), un garage plus grand (+257M$), un centre d’attachement des trains qui n’était pas nécessaire à Laval (+112M$) et des contraintes techniques liées aux travaux en milieu urbain (+89M$).
La STM a aussi provisionné 403M$ pour faire face à certains risques, tels que des terrains plus contaminés que prévu ou des retards liés aux expropriations. Une marge de 344M$ a aussi été budgétée pour avoir une marge de manoeuve selon le choix du mode de réalisation.
S’il accueille positivement les explications de la STM, Richard Bergeron s’interroge. «À ma connaissance, c’est la première fois qu’on invoque dans des calculs le coût financiers des emprunts. À ce moment là, combien a coûté le pont Champlain ou l’échangeur Turcot?», s’est-il demandé lundi en entrevue avec Métro.
M. Bergeron maintient que ces 3,9G$ rapporteront bien peu en terme d’accroissement de l’achalandage et que pour une somme équivalente, on pourrait obtenir plus de 65km d’un système tram-train comme à Ottawa ou Toronto, et qui permettrait de relier au moins six quartiers au réseau de métro.
Une opinion partagée par l’analyste en transport Réjean Benoit. Selon lui, les certains coûts, notamment ceux liés aux risques et au mode de conception, sont très élevés et démontrent qu’ils est «insensé de dépenser 3,9G$ pour cinq petites stations hors du centre-ville». Il souligne qu’un projet de tramway de 23km tel que celui de Québec coûte en comparaison deux fois moins cher alors qu’il est quatre fois plus long.